2021-07-27
What I always mistake about minimum spanning tree (MST) with Prim's algorithm
Summary
This is a post for a brief explanation of the algorithm. This is a note mainly for what I always mistake when solving the minimum spanning tree (MST) using Prim's algorithm. Thus, it will shortly focus on the algorithm and try to look more at what we have to be careful.
What is Minimum Spanning Tree(MST)?
When you are given a graph that is acyclic(no-cycle),
- It goes all the noes in the graph
- No cycle in the tree
- The cost(weight) is minimum
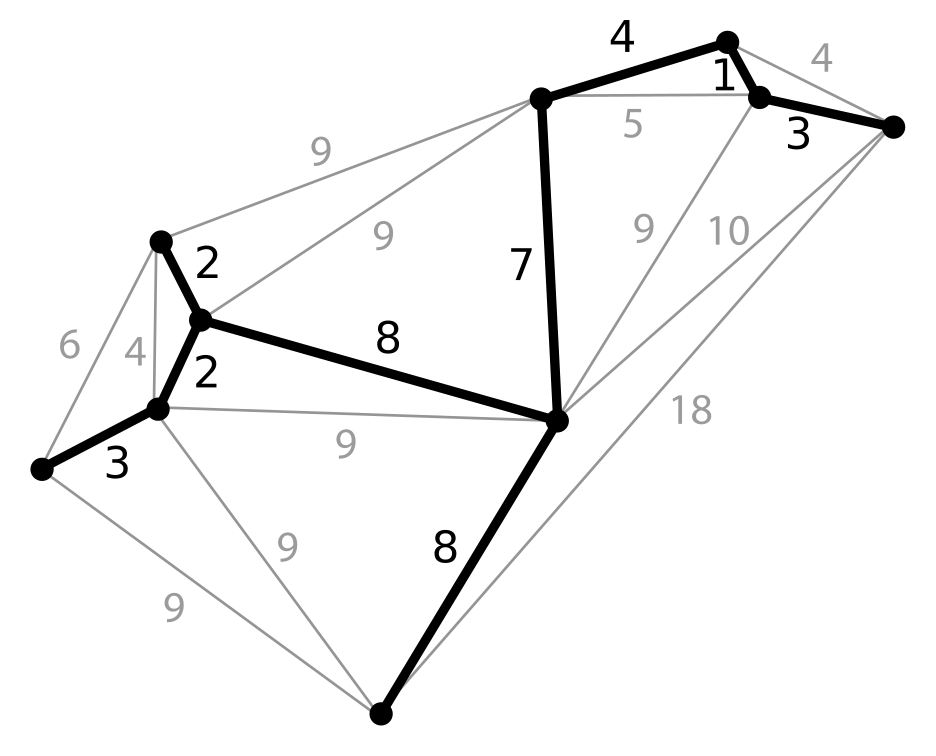
(Cited from Wikipedia)
What is Prim's algorithm?
Concept
- Basically, uses greedy with
PriorityQueue - We focus on "Node" (technically edge)
- We always try to select the node which costs a minimum to go there
- in other words, we always try to select the lowest cost edge
 (Cited from Wikipedia)
(Cited from Wikipedia)
Flow(Sudo code)
- Select one node (any node is ok) and enqueue to the PriorityQueue(
pq)- what you enqueue is (node, cost from the previous node -> to the node).
- Dequeue from the
pqas current nodecur_node - If you already visited the node, ignore
- Otherwise, mark as "visited" for
cur_node - Also, append the node to the array which represents the MST.
- Otherwise, mark as "visited" for
- Look at all nodes(
next_node) that are adjacent tocur_node- Enqueue each
next_nodeto thepqas (next_node, costcur_node-next_node).
- Enqueue each
- Loop 2-4 until
pqgets empty
Important!
The queue of pq can be (cur_node, cost) or (pre_node, cur_node, cost). It depends on what you want about MST. If you need the whole MST tree, you need both pre_node and cur_node to create an edge. If you need cost only, just cur_node is ok. This is why the queue could be both "Node" and "Edge", and this is the reason that most article describes Prim focuses on "node", wheres actually some people uses edge.
Optimization
You don't have to loop until pq gets empty. We can stop if we can know we go all noes. How do we assume? If we keep MST as an array, we can know the size of MST. Since MST goes all nodes only once, the length of the MST is exactly the same as the number of vertexes.
Thus, we can stop loop when len(pq) == #all nodes
What I always mistake and have to be careful
- PQ can be node or edge. The queue is ([pre_node(optional)], cur_node, cost from pre to cur)
- You can stop loop when you went all noes.
len(pq) == #all nodes - "Right After" dequeue from PQ, we check if visited, and mark as visited
Code sample
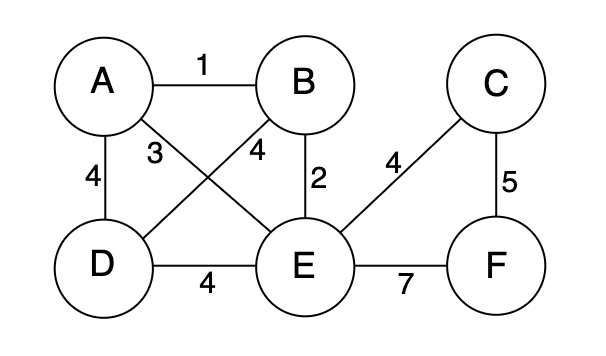 (Cited from Wikipedia)
(Cited from Wikipedia)
The input graph is the same to which is in the photo.
import heapq
adj_graph = {
'A': [(1,'B'), (4,'D'), (3,'E')],
'B': [(1,'A'), (4,'D'), (2,'E')],
'D': [(4,'A'), (4,'B'), (4,'E')],
'E': [(3,'A'), (2,'B'), (4,'D'), (4,'C'),(7,'F')],
'C': [(4,'E'), (5,'F')],
'F': [(3,'C'), (5,'E'), (7,'D')],
}
def findMst(graph):
# prepare visited
visited = {}
for key in adj_graph:
visited[key] = False
# This is for calc cost
total_cost = 0
count = 0
# (cost, cur_node)
# heapq in python looks first element as priority
pq = []
heapq.heappush(pq, (0, 'A'))
while pq:
cur_cost, cur_node = heapq.heappop(pq)
# Check and mark
if visited[cur_node]:
continue
visited[cur_node] = True
total_cost += cur_cost
# if all visited? -> stop
count += 1
if count == len(adj_graph):
return total_cost
# look around
for next_cost, next_node in adj_graph[cur_node]:
heapq.heappush(pq, (next_cost, next_node))
print(findMst(adj_graph)) #16